数学是中小学生最大的拉分学科。
很多孩子在数学学习上要么是一筹莫展,要么是不正确层出不穷,爸爸妈妈也跟着吃哑巴亏。为什么很多人觉得的数学多么的艰难呢?
元凶就是把数学当做算术在学习!

01.一个典型的误区——数学=测算
cctv新闻曾做过关于高考的调研,结论有七成网民适用高考取消数学,撤销派的观点是“日常生活可以使用数学的唯一场地便是农贸市场”。这批人该是高考考试被刷下去的那群人,而被数学避而不见就是这样的典型性的认知误区:数学=测算。
- 数学和算术看起来同样,其实并不是一回事儿。
算术仅仅数学的一部分,准确的说是数学学习的一个专用工具。
算术的目的是得到正确的结论,而数学更注重获得结果的推理过程,算术追求的是计算的准确性,而数学追求的是逻辑的准确性。算术为生活服务类,可是数学要为解决困难服务项目。
学习培训算术的关键是:记牢方法和公式计算,随后坚持练习提高速度和准确度。这也是中小学生尤其是一二年级孩子学习培训数学的模式,由于一二年级主要考察的就是计算水平。
等到了小学高年级,乃至普通高中,解题过程就会变得更加关键,纯粹借助计算水平和死记硬背的已经不能学精数学了。
02.简易公式计算背后的逻辑思维
例如,在预估23×15时,假如心算下不出来了,我们会列举下面的式子开展笔算:
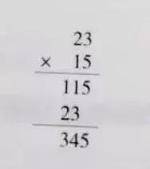
可是你有没有疑惑过为何用这个方法就可以得到正确的答案呢?我觉得,这一背后是有着有关进位的问题。
“23”意味着“2个10”和“3个1”,这一中小学生们都懂,可是我们还需要知道是这世界上不只有十进制。
比如我们了解电子计算机应用了二进制;也有十二进制,例如长度计量单位1英寸相当于12英尺,1先令相当于12美分;也有六十进制,例如时长1个小时相当于60min……
- 再比如数学题中的“网络红人担任”——“鸡兔同笼问题”。
“鸡兔同笼问题”是中国古算书《孙子算经》中著名的数学难题:“今有雉(鸡)同笼,上面有三十五头,底下九十四足。问雉兔各几何图形。”

见到这个题目,做为成年人,我们首先想的就是带入方程式,例如带到一元一次方程:
解:设兔有x只,则鸡有(35-x)只。
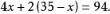
解手

鸡:35-12=23(只)
解:设鸡有x只,则兔有(35-x)只。
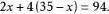
解手
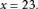
兔:35-23=12(只)
答:兔子有12只,鸡有23只。
要是没有方程式,你还能正确的解出来这题吗?
这就是典型的专用工具逻辑思维,我们用专用工具代替了思索,遇到困难就开始列方程,一旦并没有方程式可以用,我们便不容易克服了。实际上,摆脱困境的方法是有十几种不仅。
- 例如,应用假设法。
假定是一种重要的数学思维模式,先假设一种情况或结论,再通过推论、认证来解决问题,这个过程能够培养学生的思维能力。鸡和兔的脚的只数不一样是学生在解决“鸡兔同笼”问题时最大的知觉障碍,但是我们能够假定笼里全是鸡,运用头、脚排列与组合,开展发散思维摆脱困境。
假定全是鸡:2×35=70(只)
鸡爪比总脚数少:94-70=24 (只)
兔子比鸡多的是脚数:4-2=2(只)
兔子的只数:24÷2=12 (只)
鸡的只数:35-12=23(只)
假定都是兔子:4×35=140(只)
兔子脚比数量多:140-94=46(只)
兔子比鸡多的是脚数:4-2=2(只)
鸡的只数:46÷2=23(只)
兔子的只数:35-23=12(只)
- 例如由于他走红的“抬腿法”:
倘若让鸡伸出一只脚,兔子伸出2只脚,也有94÷2=47(只)脚。笼子里的兔就比鸡的脚数大1,这时候,脚与头的总数之差47-35=12,便是兔子的只数。
我们能有很多方式摆脱困境,每一种解题技巧意味着一种思维模式和解决问题途径。假如我们只是用一种工具理性逻辑思维来学习数学,尽管相同的打法能解除许多类似的题目,但是遇到未知的难题你也就不知道该如何是好了。
依据一道题目的打法,拓宽出适用于各种问题的解决方式,才是学习数学的意义。
将来,伴随着人工智能的普及化,单一化工作中将会越来越多的被设备做取代,而将来最需要的水平就是解决问题的能力,学习培训数学,是为了发展趋势这类处理各种各样问题的能力。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。


