关于本文多元正态分布推断(Inference for a Multivariate Normal Population)理论参见《Applied Multivariate Statistical Analysis and Related Topics with R》第五章内容,书中提供了相关示例的R代码,对于偏爱Python的我,希望通过Python得到同样的结果。
数据集的获取网址:
www.stat.ubc.ca/~lang/text.
示例用到的数据集分别为:class.dat2, consum2000.txt, consum2010.txt.
进行Python编程分析前,先把数据集通过R软件转换下格式,虽然Python也可以读取txt文件,但我更喜欢读取csv格式,所以通过以下代码,将数据集转换为CSV格式并保存本地。
data = read.table(\'class.dat2\', header = T)
write.csv(data, \'class.csv\')示例1
需要用到class数据集,这个示例可以简单概括为期中考试前有两次测试quiz1和quiz2,期中考试后有两次测试quiz3和quiz4,比较quiz1和quiz2之间学生成绩有无进步,以及quiz3和quiz4之间学生成绩有无进步。令μ1 = mean(quiz1 – quiz2), μ2 = mean(quiz3 – quiz4)。
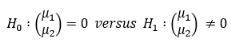
进行多元正态分布推断,编程思路为:
1.导入数据 -> 2.求解样本均值和样本协方差阵 -> 3.计算Hotelling’s T 统计量 -> 4.计算p值,根据p值结合实例分析结果。
代码实现如下:
# 引入第三方库
import pandas as pd
import numpy as np
from scipy import stats
# 读取数据
data = pd.read_csv(\"class.csv\")
df = pd.DataFrame(data)
# 构建矩阵
y = np.c_[df.quiz1-df.quiz2, df.quiz3-df.quiz4]
print(y)
# 计算样本数量n
n = np.shape(y)[0]
# 计算变量数目p
p = np.shape(y)[1]
# 计算样本均值
y = pd.DataFrame(y)
y_bar = y.mean()
print(y_bar)
# 计算样本协方差
S_y = y.cov()
print(S_y)
# 计算 Hotelling\'s T statistic
T_sq = n * np.dot(np.dot(y_bar.T, np.linalg.inv(S_y)), y_bar)
T_sq2 = ((n - p)/(p * (n - 1))) * T_sq
print(\'T_sq2:\', T_sq2)
# 计算p值
p_value = 1 - stats.f.cdf(T_sq2, p, n-p)
print(\'p_value:\', p_value)输出结果:
p_value: 0.05442091231270707由p值可以看出quiz1和quiz2之间、quiz3和quiz4之间存在一些差异,但是这些差异在5%水平不是统计显著的。
示例2
需要用到consum2000, consum2010两个数据集,这个示例可以简单概括为比较2000年和2010年在食品(Food)、衣物(Cloth)、居民数(Resid)、交通(TranC)以及教育(Educ)消费结构有无变化。令
μ1 = mean(Food.2010 – Food.2000);
μ2 = mean(Cloth.2010 – Cloth.2000);
μ3 = mean(Resid.2010 – Resid.2000);
μ4 = mean(TranC.2010 – TranC.2000);
μ5 = mean(Educ.2010 – Educ.2000).
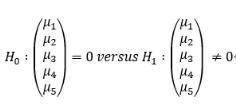
代码实现:
# 引入第三方库
import numpy as np
import pandas as pd
from scipy import stats
# 导入数据
consum00 = pd.read_csv(\"consum2000.csv\")
consum10 = pd.read_csv(\"consum2010.csv\")
# 计算2010年支出份额
data10 = consum10.iloc[:, 1:9]
sum10 = data10.sum(axis=1)
X = data10.div(sum10, axis=\'rows\')
print(X)
# 计算2000年支出份额
data00 = consum00.iloc[:, 1:9]
sum00 = data00.sum(axis=1)
Y = data00.div(sum00, axis=\'rows\')
print(Y)
# 求X与Y之差
XY_d = np.c_[X.iloc[:, 0:3]-Y.iloc[:, 0:3], X.iloc[:, 5:7]-Y.iloc[:, 5:7]]
XY_d = pd.DataFrame(XY_d, columns=(\'Food\', \'Cloth\', \'Resid\', \'TranC\', \'Educ\'))
# 计算样本均值
d_mean = XY_d.mean()
print(d_mean)
# 计算样本协方差阵
d_S = XY_d.cov()
# 计算样本大小
n = np.shape(XY_d)[0]
# 计算变量数
p = np.shape(XY_d)[1]
# 计算 Hotelling\'s T 统计量
T2 = n * np.dot(np.dot(d_mean.T, np.linalg.inv(d_S)), d_mean)
Tstar2 = ((n-p)/(p*(n-1)))*T2
# 计算p值
p_value = 1 - stats.f.cdf(Tstar2, p, n-p)
print(\'p_value:\', p_value)输出结果:
p_value: 7.460698725481052e-14可见p值近似为0,拒绝原假设,说明2000年与2010年的消费结构发生了明显的变化。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。


